ECE4960-2022

Course on "Fast Robots", offered Spring 2022 in the ECE dept at Cornell University

This project is maintained by CEI-lab

Cornell University: ECE 4960 / 5960

Return to main page

Lab 9: Mapping

Objective

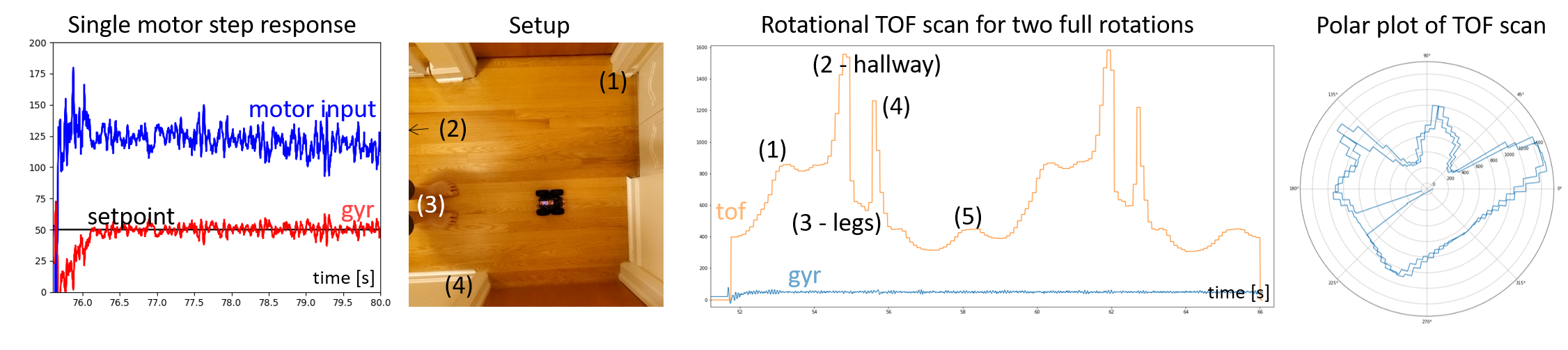
The purpose of this lab is to build up a map of a static room (in this case the front room of the lab); you will use this map in later localization and navigation tasks. To build the map, you will place your robot in a couple of marked up locations around the lab, and have it spin around its axis while measuring the ToF readings.

The quality of your map will depend on how many readings you manage to obtain during a rotation and how accurately they are spaced out in angular space. If you choose to do PID control on the raw gyroscope values, aim to make the robot drive as slow as possible. If you choose to do PID control on orientation (i.e. integrated gyroscope values), aim to make the robot rotate in as small increments as possible, then stop and measure. When you have all the readings, you will merge them together using transformation matrices, plot them, and then use these to draw up the map using straight line segments.

Parts Required

Prelab

Consider checking out lecture 2 on transformation matrices again.

PID Control

As mentioned, you can complete your PID control for on-axis turns in two ways:

  1. Orientation control: If you choose this option, create a PID controller that allows your robot to do on-axis turns in small, accurate increments.
    • Aim for at least 14 readings (roughly 20 degree increments) per 360 degree rotation.
    • This option is easier than the other if you have already completed Task B in Lab 6.
    • This option may also be best if you cannot get your robot to do slow reliable turns. Recall that the ToF sensor will report false outputs if the distance to the object changes too drastically during a reading, but when you sit still you guarantee that the TOF sensor is pointing towards a fixed point in space.
    • Please quantify and/or use graphs to document that your PID controller works well, and upload a video that shows if your robot turns (roughly) on axis.
    • Given the drift in your sensor, the size and accuracy of your increments, and how reliably your robot turns on axis, reason about the average and maximum error of your map if you were to do an on-axis turn in the middle of a 4x4m square, empty room.
  2. Angular speed control: If you choose this option, create a PID controller that works directly on the raw gyroscope values. This is beneficial over orientation control, because you avoid accumulating errors during integration.
    • Try to aim for a maximum of 25 degrees per second, as this will allow you to do 14 sensor readings spaced out by approximately 1s. (This may be too hard given your particular robot; a higher angular speed is fine, as long as your map comes out reasonable).
    • You will likely need to low pass filter the gyroscope values - read up on how we did that with a complementary LPF in Lecture 4, slide 23.
    • You can also consider adjusting the integration time of the TOF sensor, using proximitySensor.setProxIntegrationTime(4); //A value of 1 to 8 is valid. Note that his function is only available in the Tof Pololu library.
    • One way to make the robot spin even slower is to block one set of wheels while turning the others. This means that your robot is now driving in a slight circle (rather than on-axis), which will make post-processing of data slightly more difficult, but allow you to capture data more reliably.
    • Please quantify and/or use graphs to document that your PID controller works well, and upload a video that shows how your robot turns.
    • Given the slowest speed you are able to achieve, how much does the orientation of the robot change during a single measurement? If you were spinning in the middle of a 4x4m2 empty, square room, what kind of accuracy can you expect?

Read out Distances

  1. Execute your turn at each of the marked positions in the lab space. (If you are low on time, doing this in the Phillips hallway or at home to show that your concept works is okay).
    • During the turn, measure the distance using a ToF sensor mounted in the front of the robot. When the turn is completed return the data to the computer over Bluetooth. If you have a distance sensor placed on the side of the robot, you are welcome to add those readings to your turn.
    • To make it easier on yourself, start the robot in the same orientation in all scans.
    • Consider whether your robot behavior is reliable enough to assume that the readings are spaced equally in angular space, or if you are better off trusting the orientation from integrated gyroscope values.

  2. Sanity check individual turns by plotting them in polar coordinate plot. For simplicity assume that the robot is rotating in place. Do the measurements match up with what you expect?

  3. Try rotating twice or more to see how precise your scans are.

Below you can see an example of angular speed control, a scan of a hallway, and TOF output plotted over time and in a polar plot.

TO BE ADDED: ACTUAL MAP OF THE LAB SPACE!

Merge and Plot your readings

Compute the transformation matrices and convert the measurements from the distance sensor to the inertial reference frame of the room (these will depend on how you mounted your sensors on the robot.)

Below you can see an example of an office scan, with approximate walls drawn on top.

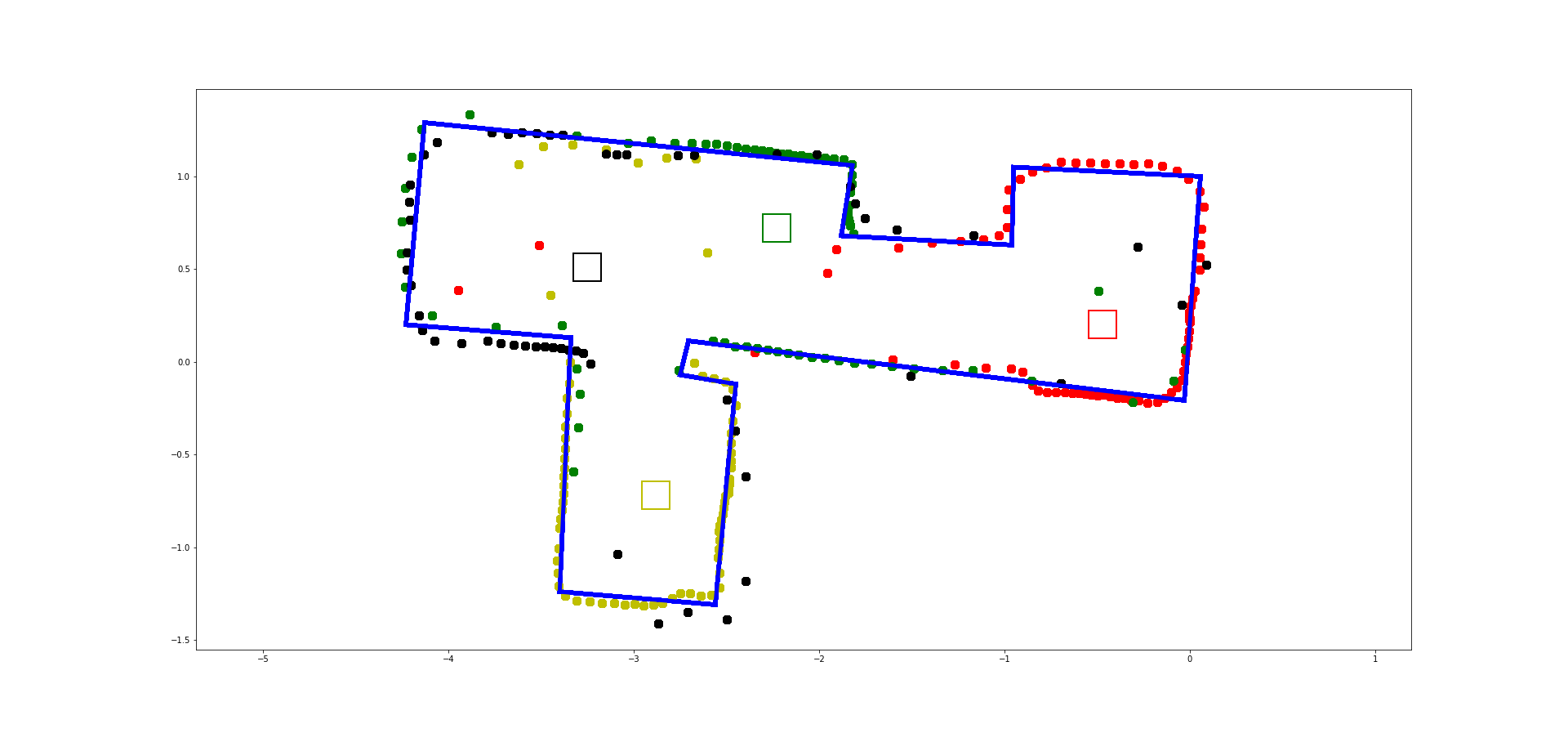
Convert to Line-Based Map

To convert this into a format we can use in the simulator, manually estimate where the actual walls/obstacles are based on your scatter plot. Draw lines on top of these, and save two lists containing the end points of these lines: (x_start, y_start) and (x_end, y_end). In the next lab, we will import these lists into the simulator.

Write-up

To demonstrate that you’ve successfully completed the lab, please upload a brief lab report (<1.000 words), with code snippets (not included in the word count), photos, graphs, and/or videos documenting that everything worked and what you did to make it happen.